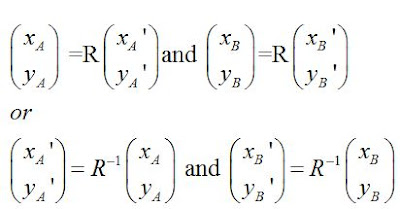Landing Activities: Integrating factor

link to the activity here

Why does the "separation of variables" work with O.D.E. of the 1st order?

The full article here

Reflection in line y=mx matrix

What it follows is a proposal for deriving the linear transformation matrix for reflection across the line y=mx matrix. 
Let’s  X’OY’  a new set coordinate axis which comes after XOY has rotated around O at an angle θ. Where θ=arctan(m). In this new coordinate axis , the line y=mx coincides with the OX’ axis, so the transformation matrix for the reflection in OX’ axis is :

Let A a point on our plane and B’ its reflection in OX’ axis (which is actually the line y=mx).

These points have coordinates

We know that:

The Arc as a locus on the Argand plane :an example.

The following example is actually the question 12, of the exercise 3B which is in the A2 Further Pure Mathematics textbook (MEI STRUCTURED MATHEMATICS)