What it follows is a proposal for deriving the linear transformation matrix for reflection across the line y=mx matrix.
Let’s X’OY’ a new set coordinate axis which comes after XOY has rotated around O at an angle θ. Where θ=arctan(m). In this new coordinate axis , the line y=mx coincides with the OX’ axis, so the transformation matrix for the reflection in OX’ axis is :
Let A a point on our plane and B’ its reflection in OX’ axis
(which is actually the line y=mx).
These points have coordinates 
We know that:



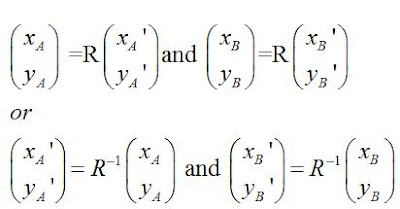









No comments:
Post a Comment